Metal Spintronics

Overview

Spintronics has emerged as an active field of research that aims at the development of a new generation of devices relying on the manipulation of the electron’s spin. In this research line, we focus on the study of spin-orbit coupling-related phenomena, such as the spin Hall effect in heavy metals, the Rashba-Edelstein effect in interfaces, and the spin-momentum locking in topological insulators, which we study in metallic nanodevices. These phenomena allow electrical spin-charge current interconversion, giving rise to interesting applications such as the spin-orbit torques to write magnetic memories or the integration of magnetic memory and spin-based logic, as recently proposed by Intel Corp. [1]. In addition, we are using heavy metal/magnetic insulator heterostructures to explore the interplay between electron spins and magnon spins, such as the spin Hall magnetoresistance and the magnon transport in nonlocal devices. Using state-of-the-art nanofabrication, our main goal is to devise alternative geometries that unlock innovative architectures for spin-based computational devices.

 

Research directions

Spin-charge conversion in metallic lateral nanostructures

One of the core elements of a spintronic device lies on the manipulation of pure spin currents. Using lateral spin valves composed of Cu and ferromagnetic NiFe nanowires, we have studied the generation and transport of pure spin currents [2]. We use the spin absorption technique by adding nanowires made of heavy metals [3-5], ferromagnets [6] or Rashba interfaces [7], which absorb the pure spin current and convert it to charge current, allowing us to quantify spin-charge current conversion phenomena such as the spin Hall effect or the Rashba-Edelstein effect. Now, we are exploring these concepts in alternative systems with large spin-orbit coupling, including topological insulators and other exotic materials.

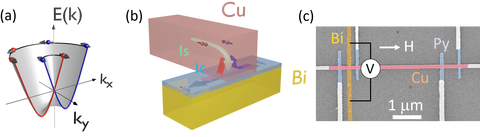
Spin-charge current conversion in a Rashba system. (a) Rashba energy dispersion for a 2DEG. (b) Schematic of the inverse Rashba-Edelstein effect occurring in the spin absorption method. (c) Colored SEM image of a typical device to measure the spin-to-charge current conversion.

 

Local spin detection for spin-orbit-based effects

Spin-polarized currents generated at ferromagnetic/non-ferromagnetic interfaces can be detected by SOC-based effects as voltage and current outputs. With the favorable miniaturization recently proposed for magnetoelectric spin–orbit logic devices (MESO) in mind [1], we elaborate the scaling laws and understand comprehensively the mechanisms of spin-charge conversion in such devices [8]. In collaboration with Intel Corp, we are now seeking new SOC systems/materials that can produce large enough output voltages to reach the requirements of the MESO device [1].

 

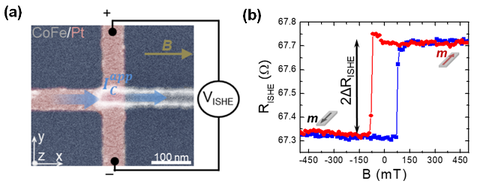
Spin-orbit magnetic state readout with a giant inverse spin Hall signal. (a) SEM image of a local spin detection device with the measurement configuration for the spin-to-charge current conversion (inverse spin Hall effect). (b) An observation of giant inverse spin Hall signal in CoFe/Pt system.

 

Spin Hall magnetoresistance

The use of magnetic insulators is attracting a lot of interest due to a rich variety of spin-dependent phenomena with potential applications for spintronics devices, such as the spin Hall magnetoresistance (SMR). SMR is based on the interaction between the surface magnetic moments of the magnetic insulator and the spin accumulation in materials with strong spin-orbit coupling (Pt, Ta, Au, W, etc.). In our group, we use this effect to characterize a variety magnetic insulators with complex surface magnetism, including ferrimagnetic spinels [9, 10], ferrimagnetic garnets [11,12], or ferromagnetic perovskites [13]. Within this framework, we have discovered Hanle magnetoresistance, a related effect where the spin accumulation directly interacts with the applied magnetic field [14].

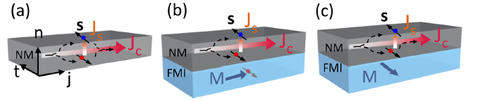
Working principle of SMR. (a) Metallic layer with strong spin-orbit coupling (NM), with a charge current jc flowing along j. A spin current js along n with spin polarization s along t is created due to spin Hall effect. The spin current is reflected back at the surfaces, generating additional charge current due to inverse spin Hall effect. (b) NM/ferromagnetic insulator (FMI) bilayer where the magnetization in the FMI is perpendicular to s. In this case, the spin current will be absorbed at the NM/FMI interface. (c) When the magnetization is parallel to the spin polarization, the spin current will be reflected. The difference in resistance between (b) and (c) leads to SMR.

 

Magnon transport

Transport of spin angular momentum via the propagation of magnons has been demonstrated in the ferrimagnetic insulator Y3Fe5O12 (YIG) [15, 16]. Recent experiments show that magnon spin currents (diffusive magnons carrying spin angular momentum) can be excited electrically or thermally and detected electrically in a non-local geometry with Pt electrodes [11,16-18]. Interestingly, these magnon spin currents have been reported to propagate in YIG to much longer distances (~1-100 μm at room temperature) [11,16-18] than electron spins in light metals such as Cu or Al (~300 nm at room temperature), thus providing a new powerful method to transport spin information.

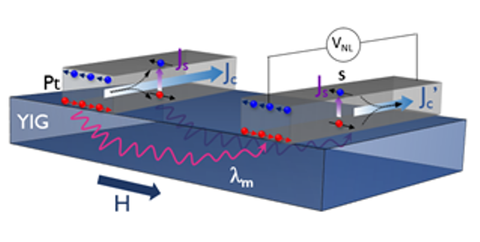
Schematic representation of the excitation, transport and detection of magnons in a non-local device under electrical excitation.

References

[1] S. Manipatuni ,D.E. Nikonov, C.-C. Lin, T. A. Gosavi, H.Liu, B. Prasad, Y.-L. Huang, E. Bonturim, R.Ramesh, and I. A. Young, Nature 565, 35 (2019). 

[2] E. Sagasta, Y. Omori, M. Isasa, Y. Otani, L. E. Hueso, and F. Casanova, Appl. Phys. Lett. 111, 082407 (2017).

[3] M. Isasa, E. Villamor, L.E. Hueso, M. Gradhand, and F. Casanova, Phys. Rev. B  91, 024402 (2015).

[4] E. Sagasta, Y. Omori, M. Isasa, M. Gradhand, L. E. Hueso, Y. Niimi, Y. Otani, and F. Casanova, Phys. Rev. B 94, 060412 (R) (2016).

[5] E. Sagasta, Y. Omori, S. Vélez, R. Llopis, C. Tollan, A. Chuvilin, L. E. Hueso, M. Gradhand, Y. Otani, and F. Casanova, Phys. Rev. B 98, 060410 (R) (2018).

[6] Y. Omori, E. Sagasta, Y. Niimi, M. Gradhand, L. E. Hueso,  F. Casanova, and Y. Otani, Phys. Rev. B 99, 014403 (2019).

[7] M. Isasa, M.C. Martínez-Velarte, E. Villamor, C. Magén, L. Morellón, J.M. De Teresa, M.R. Ibarra, G. Vignale, E.V. Chulkov, E.E. Krasovskii, L.E.  Hueso, and F. Casanova, Phys. Rev. B  93, 014420 (2016).

[8] V. T. Pham, I. Groen, S. Manipatruni, E. Sagasta, C.-C. Lin, T. Gosavi, A. Marty, L. E. Hueso, I. Young, and F. Casanova, submitted (2019).

[9] M. Isasa, A. Bedoya-Pint, S. Vélez, F. Golmar, F. Sánchez, L. E. Hueso, J. Fontcuberta and F. Casanova, Appl. Phys. Lett. 105, 132406 (2014).

[10] M. Isasa, S. Vélez, E. Sagasta, A. Bedoya-Pinto, N. Dix, F. Sánchez, L. E. Hueso, J. Fontcuberta, and F. Casanova, Phys. Rev. Appl. 6, 034007 (2016).

[11] S. Vélez, A. Bedoya-Pinto, W. Yan, L. E. Hueso and F. Casanova, Phys. Rev. B 94, 174405 (2016).

[12] J. M. Gomez-Perez, S. Vélez, L. McKenzie-Sell, M. Amado, J. Herrero-Martín, J. López-López, S. Blanco-Canosa, L. E. Hueso, A. Chuvilin, J. W. A. Robinson and F. Casanova, Phys. Rev. Appl. 10, 044046 (2018).

[13] S. Vélez, V. N. Golovach, J. M. Gomez-Perez, C. T. Bui, F. Rivadulla, L.E. Hueso, F. S. Bergeret, and F. Casanova, arXiv:1805.11225.

[14] S. Vélez, V. N. Golovach, A. Bedoya-Pinto, M. Isasa, E. Sagasta, M.Abadia, C. Rogero, L. E. Hueso, F. S. Bergeret, and F. Casanova, Phys. Rev. Lett. 116, 016603 (2016).

[15] Y. Kajiwara, K. Harii, S. Takajashi, J. Ohe, K. Uchida, M. Mizuguchi, H. Umezawa, H. Kawai, K. Ando, K. Takanashi, S. Maekawa and E. Saitoh, Nature 464, 08876 (2010).

[16] L. J. Cornelissen, J. Liu, R .A. Duine, J. Ben Youssef and J. van Wees., Nat. Phys. 11, 1022 (2015).

[17] B. L. Giles, Z. Yang, J. S. Jamison. J. M. Gomez-Perez, S. Vélez, L. E. Hueso, F. Casanova and R. C. Myers, Phys. Rev. B 96, 180412(R) (2017).

[18] J. M. Gomez-Perez, S. Vélez, L. E. Hueso and F. Casanova, in preparation (2019).