Critical Scaling of Dynamic Phase Transitions in magnetic films
In a recent article published in Physical Review Letters (Phys. Rev. Lett. 131, 116701 (2023)) and selected as an Editor’s suggestion, Mikel Quintana and Andreas Berger from the Nanomagnetism group at nanoGUNE succeeded in experimentally detecting and quantifying critical scaling near the dynamic phase transition (DPT) for the first time.
While this type of non-equilibrium phase transition and its associated order parameter scaling have been theoretically investigated for decades, prior experiments have been unsuccessful in characterizing critical scaling. Thus, the now published experimental results by Quintana and Berger [1] close a very important gap in the knowledge of dynamic phase transitions and put existing model calculations on solid footing, also because the experiments revealed 2D Ising model type behavior as predicted for the symmetry class of the magnetic thin film samples that the authors investigated.
The study of dynamic behavior and kinetic pattern formation in interacting systems is a crucially important aspect of science, given that they are present in such diverse areas such as laser emission, the formation of sand dunes or brain activity. Correspondingly, the study of non-equilibrium dynamic phenomena is of utmost importance, and its detailed and quantitative understanding crucially relies on appropriate models. One of these models is the widely used kinetic Ising Model (kIM), which can exhibit qualitatively different types of dynamic behavior, including dynamic phase transitions, despite its simplicity. After more than three decades of research using the kIM, consensus emerged that the properties of DPTs are truly analogous to those of thermodynamic phase transitions (TPTs), including their critical scaling behavior. However, these conclusions are based on theoretical investigation only, given that no comparable experimental results were available until the now published work by Quintana and Berger [1].
Key experimental advances in the work of Quintana and Berger were the highly sensitive detection of real-time magnetization behavior by means of a unique and patented magneto-optical detection system and the design, fabrication and identification of suitable samples with in-plane uniaxial anisotropy, mimicking the Ising model symmetry. Hereby, it was crucial to identify a sample thickness range, in which non-critical fluctuations in the paramagnetic regime could be suppressed, which are very prominent in the vicinity of the DPT and generally lead to a massive reduction of the critical regime, making quantitative scaling experiments for most samples impossible. Quintana and Berger identified in their work a relevant sample thickness range, in which these perturbing metamagnetic fluctuations are absent and thus allow the experimental acquisition of high-quality data sets in a sufficiently large phase space. In addition, their work postulates an equation of state for their dynamic system in analogy to the well-known Arrott-Noakes equation for equilibrium systems, and they verify its quantitative correctness, as can be seen from the data in the figure in direct comparison with the theoretically predicted behavior. Excellent agreement is observed and the measured data sets corroborate the 2D Ising model behavior that was theoretically expected to occur for this type of sample.
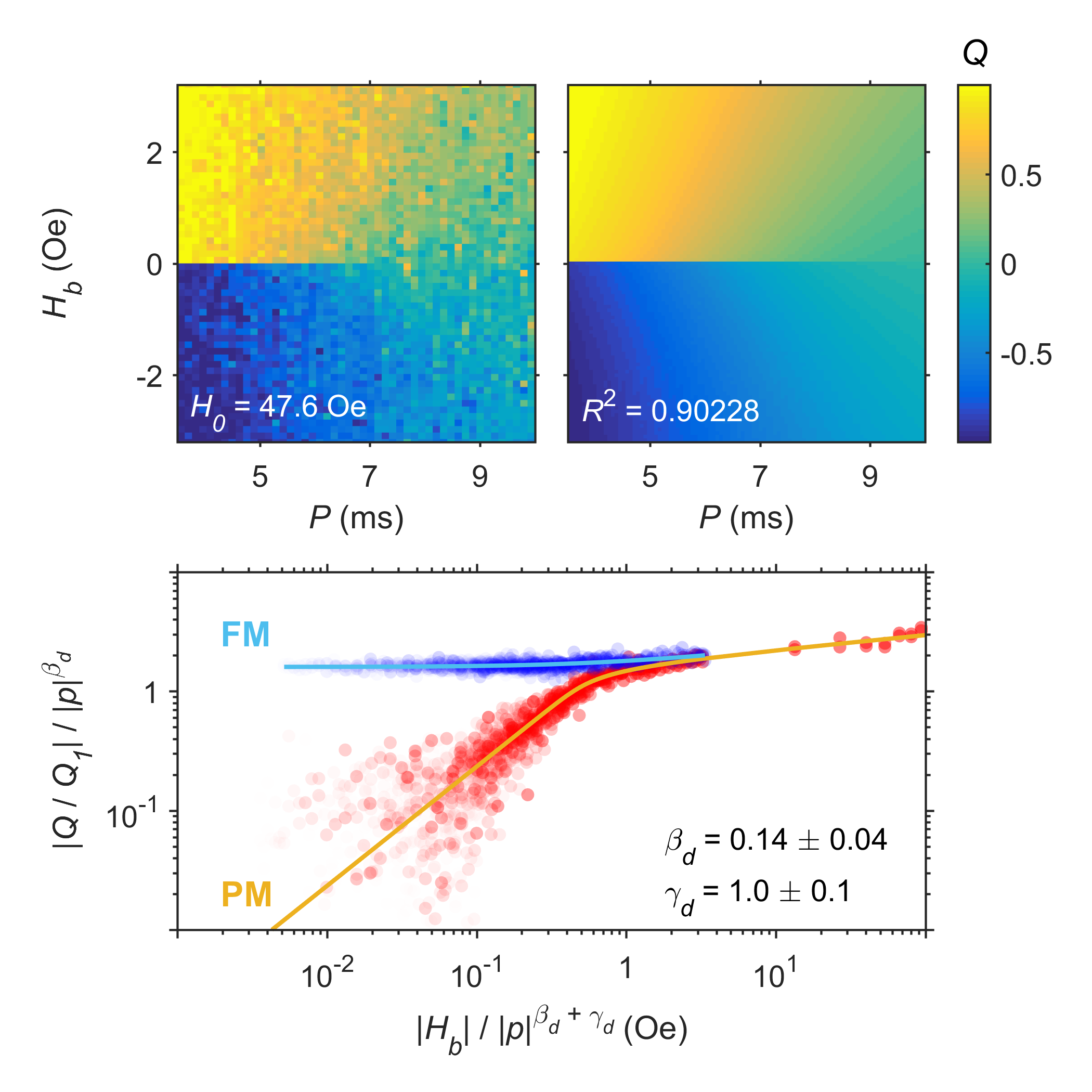
Figure: The upper two figures show as color-coded maps the phase space behavior of the dynamic magnetic order parameter Q as a function of the two relevant phase space parameters, the field oscillation period P and constant bias field Hb, which is the conjugate field of Q (the color code legend appears on the right-hand side and is valid for both figures). The left-hand color-coded map displays experimental data collected on an in-plane uniaxial Co(1010) film of 0.8 nm thickness, while the right-hand plot shows the theoretically expected behavior, postulated by the application of the dynamic analog of the Arrott-Noakes equation. The bottom figure displays the experimental data by means of an Arrott-plot, displaying the renormalized order parameter |Q/Q1|/|p|βd as a function of the renormalized field |Hb|/|p|βd+γd, showing the collapse of all data onto only two curves, one corresponding to the FM (blue) phase and one for PM (red) phase. The cyan and orange lines represent the theoretically expected ideal behavior.
Acknowledgements: We acknowledge support by the Spanish Ministry of Science and Innovation under the Maria de Maeztu Units of Excellence Programme (Grant No. CEX2020-001038-M), Project No. RTI2018-094881-B-100 (MCIU/Feder), and predoctoral fellowship No. PRE2019-088428.
